LLaMA 3/2/1模型结构总览

青稞2024-05-092024-05-09

作者：孟繁续，北京大学博士生，研究方向 LLM（大型语言模型）和模型压缩
主页：fxmeng.github.io
声明：原文已经授权，版权归原作者！
原文：https://zhuanlan.zhihu.com/p/636784644

LLaMA-3又出来了，综合表现非常惊艳，我在实际测试中能力也比LLaMA-2-7B，Mistral-7B和Gemma-7B效果好。模型还是直接复用之前的代码，不过最小的8B模型也用上了GQA了，实测速度挺快。手头的llama-2可以丢了，可以拥抱llama-3了。

llama2 出来了，并且开源可商用，这下开源社区又要变天了。快速看一下官网以及paper，看看llamav2相比v1有什么更新吧：

预训练语料从1->2 Trillion tokens
context window 长度从2048->4096
收集了100k人类标注数据进行SFT
收集了1M人类偏好数据进行RLHF
在reasoning, coding, proficiency, and knowledge tests上表现超越MPT和Falcon
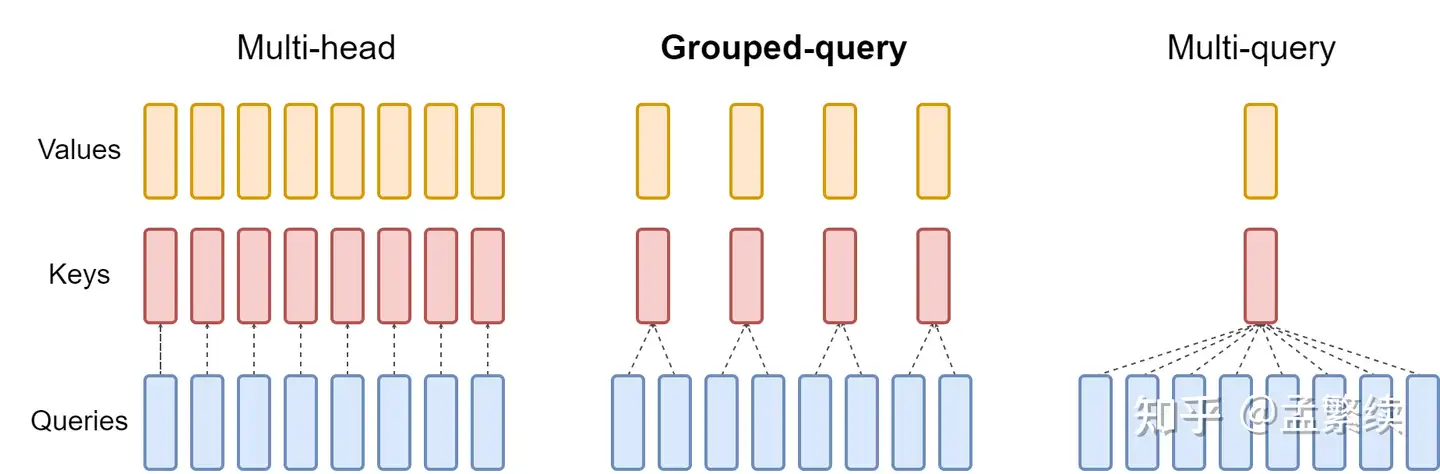
和falcon一样，使用了Group query attention，节省cache

LLaMA现在已经是开源社区里炙手可热的模型了，但是原文中仅仅介绍了其和标准Transformer的差别，并没有一个全局的模型介绍。找了找其他博客也都是和原文一样，没有介绍模型的结构总览。因此打算写这篇文章，争取让读者不参考任何其他资料把LLaMA的模型搞懂。

结构

如图所示为LLaMA的示意图，由Attention和MLP层堆叠而成：

null

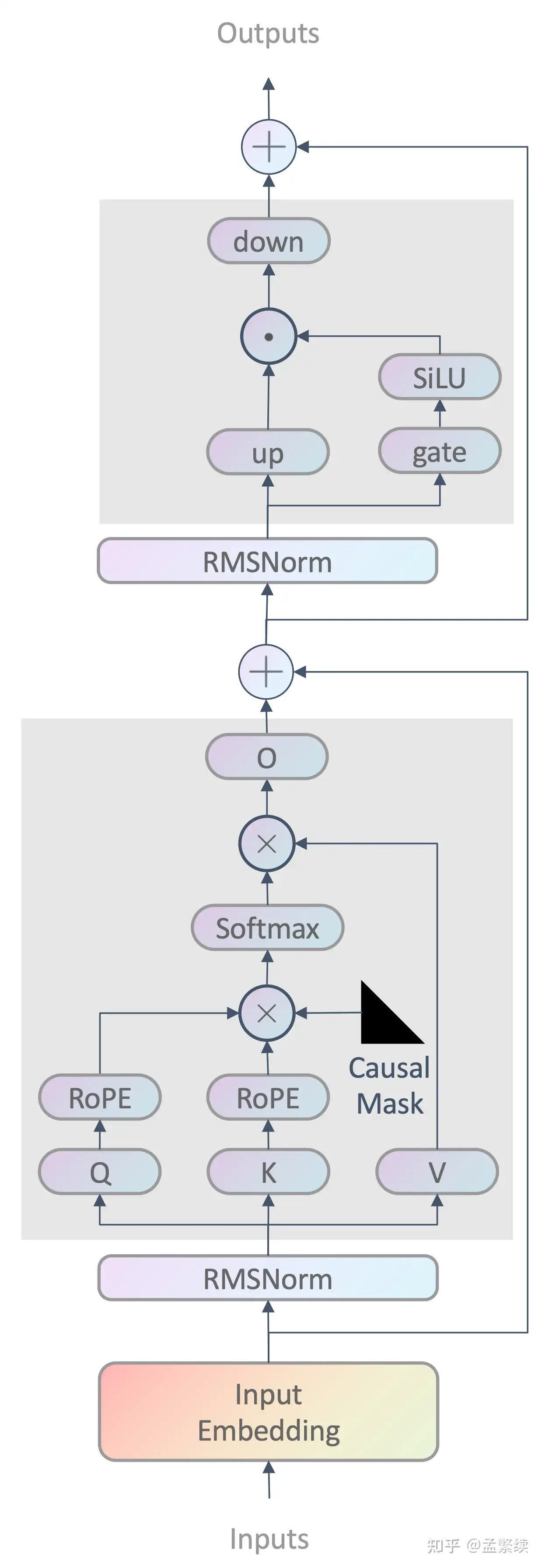
模型的主要特点为：

前置的RMSNorm，
在Q、K上使用RoPE旋转式位置编码，
使用causal mask保证每个位置只能看到前面的tokens，
LLaMA可以将更早的K、V拼接到当前K、V前面，可以用Q查找更早的信息，为了清晰没在图中画出来。
MLP表达式：\(down(up)(x) x SiLU(gate(x))\) ，其中down, up, gate都是线性层。
V2 context window 4096，使用了Group Query Attention。

LLaMA各个不同大小的结构设置如下表所示。其中最大的65B的LLaMA用了2048张80GB的A100，batch size为4百万，训练一次需要21天。

params	dimension	n heads	n layers	learning rate	n tokens	A100-hours
6.7B	4096	32	32	3.0e−4	1.0T	82432
13.0B	5120	40	40	3.0e−4	1.0T	135168
32.5B	6656	52	60	1.5e−4	1.4T	530432
65.2B	8192	64	80	1.5e−4	1.4T	530432

Group Query Attention(V2 only)

自回归模型生成回答时，需要前面生成的KV缓存起来，来加速计算。多头注意力机制(MHA)需要的缓存量很大，Multi-Query Attention指出多个头之间可以共享KV对。Group Query Attention没有像MQA一样极端，将query分组，组内共享KV，效果接近MHA，速度上与MQA可比较。p.s. 这个技术falcon已经用上了，当时falcon说自己用的是multi query attention，因为当group=1时，GQA和MQA是等价的。falcon支持设置不同的G。

null

RMSNorm

这是在BERT、GPT等模型中广泛使用的LayerNorm：

\(y=Var(x)+ϵx−Mean(x)∗W+B\)

RMSNorm(root mean square)发现LayerNorm的中心偏移没什么用(减去均值等操作)。将其去掉之后，效果几乎不变，但是速度提升了40%。最终公式为：

\(y=Mean(x2)+ϵx∗W\)

注意除了没有减均值，加偏置以外，分母上求的RMS而不是方差。

LLaMA在 Attention Layer和MLP的输入上使用了RMSNorm，相比在输出上使用，训练会更加稳定。

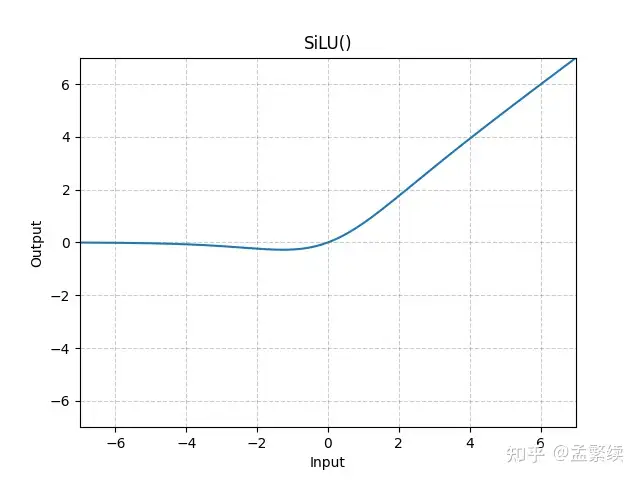
SwiGLU

LLaMA没有使用ReLU，而是使用了SwiGLU，有时也被称为SiLU。公式为： \(Sigmoid(x)∗x\) ，效果类似平滑版的ReLU：

null

RoPE

LLaMA使用了Rotary Position Embedding。对于Q的第m个位置向量q，通过以下方法注入位置编码：

\[f(q,m)=q0q1...qd/2−1qd/2qd/2+1...qd−1×cos(mθ0)cos(mθ1)...cos(mθd/2−1)cos(mθ0)cos(mθ1)...cos(mθd/2−1)+−qd/2−qd/2+1...−qd−1q0qd1...qd/2−1×sin(mθ0)sin(mθ1)...sin(mθd/2−1)sin(mθ0)sin(mθ1)...sin(mθd/2−1)\]

其中 θ 是值介于[1,0)之间的固定向量。通过以下代码得到了上式中的第二项 \(cos(mθi)\) 和第四项 \(sin(mθi)\) 。

class LlamaRotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000):
        super().__init__()
        theta = 1.0 / (base ** (torch.arange(0, dim, 2) / dim))
        t = torch.arange(max_position_mbeddings)
        freqs = torch.einsum("i,j->ij", t, theta)

        emb = torch.cat((freqs, freqs), dim=-1)
        self.register_buffer("cos_cached", emb.cos())
        self.register_buffer("sin_cached", emb.sin())

    def forward(self, seq_len=None):
        return self.cos_cached[:, :, :seq_len, ...], self.sin_cached[:, :, :seq_len, ...]

# 在LlamaAttention通过以下命令调用：
cos, sin = self.rotary_emb(seq_len=kv_seq_len)
````

以下代码将q沿着最后一个维度劈成两半，将后一半乘-1，然后连接在第一半之前，就得到了上式第三项。

```python
# 在接下来的apply_rotary_pos_emb函数里调用

def rotate_half(x):
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)

后通过以下代码得到结合了位置编码的Q,K(K和Q使用同样的方式进行位置编码)。

def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
    q_embed = (q * cos[position_ids]) + (rotate_half(q) * sin[position_ids])
    k_embed = (k * cos[position_ids]) + (rotate_half(k) * sin[position_ids])
    return q_embed, k_embed

# 在LlamaAttention中通过以下命令调用：
query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids)

使用了这么复杂的位置编码，有什么好处呢？从上面的公式可以看出，RoPE形式上是绝对位置编码，即依赖其绝对位置m。

绝对位置编码的优点是计算速度快等，缺点是拓展长度比较麻烦，且绝对位置并没有什么实际意义。而相对位置编码对学习token之间的关系很有意义，比如距离的很远的两个token之间的关联大概率很小，使用相对位置编码往往能够获得更好的效果。此外拓展长度也更容易，因为不论context size多长，只需关注最长距离以内的输入即可。相对位置编码的缺点是没有绝对位置编码计算速度快。

当我们计算Attention时，RoPE可以变成相对位置编码。

\[Attm,n=fT(q,m)×f(k,n)=(q0cos(mθ0)−qd/2sin(mθ0))(k0cos(nθ0)−kd/2sin(nθ0))+...+(qd/2cos(mθ0)+q0sin(mθ0))(kd/2cos(nθ0)+k0sin(nθ0))+...=q0k0(cos(mθ0)cos(nθ0)+sin(mθ0)sin(nθ0))+q0kd/2(−cos(mθ0)sin(nθ0)+sin(mθ0)cos(nθ0))+qd/2k0(−sin(mθ0)cos(nθ0)+cos(mθ0)sin(nθ0))+qd/2kd/2(sin(mθ0)sin(nθ0)+cos(mθ0)cos(nθ0))+...=q0k0cos((m−n)θ0)+q0kd/2sin((m−n)θ0)+qd/2k0sin((n−m)θ0)+qd/2kd/2cos((m−n)θ0)+...=q0k0q1k1...qd/2−1kd/2−1qd/2kd/2qd/2+1kd/2+1...qd−1kd−1T×cos((m−n)θ0)cos((m−n)θ1)...cos((m−n)θd/2−1)cos((m−n)θ0)cos((m−n)θ1)...cos((m−n)θd/2−1)+−qd/2k0−qd/2+1k1...−qd−1kd/2−1q0kd/2qd1kd/2+1...qd/2−1kd−1T×sin((m−n)θ0)sin((m−n)θ1)...sin((m−n)θd/2−1)sin((m−n)θ0)sin((m−n)θ1)...sin((m−n)θd/2−1)\]

从上面这个公式可以看出，q和k的attention依赖相对距离m-n。因此RoPE为q、k注入的绝对位置编码，计算得到的attention，却变成了相对位置编码。妙的很，我这里为了不参考其他文章就很容易搞懂LLaMA的结构，简化了很多东西，推荐大家看一看RoPE原作者苏剑林[1]的博客了解更多信息。

文中参考的代码是huggingface的transformers库实现的版本，并不是Meta官方的代码。受笔者水平限制，如果哪里讲的不对，或者不够清晰易懂，欢迎在评论区交流。