作者：陈陈，TSAIL: 强化学习+生成模型 原文：https://zhuanlan.zhihu.com/p/693746297 >>加入青稞AI技术交流群，与青年研究员/开发者交流最新AI技术

20号下午两位THUNLP的同学（淦渠和立凡）分别给我发了这篇arxiv，询问和上次讨论时谈到的一个理论的联系。简单看了文章后发现几乎完全撞了车。好吧严格讲也不算撞，这篇文章的理论去年十月我大概想明白推导完，但实在想不清楚有啥合适的应用因而给放弃掉了。现在也只能感慨之余写个解读了。

1
2

From r to Q∗: Your Language Model is Secretly a Q-Function
https://arxiv.org/pdf/2404.12358.pdf

为什么写这个解读：

本文几乎是DPO的原班人马搞的，新来的Joey Hejna是X-QL（本文部分核心理论）一作。这篇文章并没有提出一个新的算法，或者是在一个新的任务上刷了SOTA，主要是对DPO算法给出了一个理论解释，统一了处理LLM强化学习任务的两个视角，即序列决策还是单步决策。用强化学习的语言就是说dense or sparse reward，r or Q。而后者这个Q有不禁让人联想到OPENAI“泄露的Q*计划”。应该说还是有其理论价值的。

此外我相信本文即使对于多数专业研究者也是晦涩难懂的。这篇文章对于NLP领域的读者而言要求了太多前置的RL知识，对theoretical RL领域读者又过于应用，符号系统一定程度上被改写了。

因此本文面向NLP领域已经有了DPO和PPO算法的基本了解和实践，但不熟悉系统强化学习理论的读者。本文不采用原论文的叙述思路和符号系统，更多反应的是一些个人见解（我并不完全认可原作者的叙述方式）。主要作为看不懂原文但又希望get到原作者想表达啥的参考。

本文符号系统：

• \(y\) ：表示一个句子，一个句子有多个token组成， \(y_t\) 表示第t个token。$ y_t V$ 。 \(V\) 表示字典。我们假设所有句子的长度都是 \(T\) ，即 \(y_T = EOS\) 。
• \(\mu\) , 表示SFT阶段后得到的语言模型。 (y) 是采样句子的概率， (y_t|y_{<t}) 表示单步token采样概率, \(y_{y\leq t}\) 表示前半句话。一般而言采样句子我们还需要一个prompt x作为条件，本文忽略这个x。
• \(r(\cdot)\) ：这是一个可以给任意一个句子打标量分值的函数。它抽象地代表人类偏好。
• \(\pi^*(y) \propto \mu(y)e^{r(y)/\beta}\) .这是我们希望得到的语言模型分布。
• \(\pi_\theta\) ，这是我们实际训练的那个LLM。\(\pi_\theta\) 被初始化为 \(\mu\) ，它的优化目标是 \(\pi^*\) 。

要回答的问题：

• 为什么说LLM本质上是一个Q-function（而不仅仅是reward model）。
• 这篇文章有啥现实意义吗？新的视角可能带来哪些新的alignment研究方向（坑）：RLHF dense reward 方向以及RL的Q-learning方向。

这是我第一次尝试在知乎上写文章解读，有什么可以改进的地方还请大家多提意见。以下是征文：

一、DPO背景

我们知道DPO的loss function其实是一个训练reward model的loss。 DPO这篇论文题目也叫做Your Language Model is Secretly a Reward Model：

\(L_\text{DPO} = - \log \sigma (r_\theta(y_w) - r_\theta(y_l))\)

DPO这篇文章的核心创新在于，他说我们其实不用拿这个loss去学一个奖励模型，奖励函数模型本身不也是为了拿来训练LLM的吗？我们直接定义：

\(r_\theta(x, y) := \beta \log \frac{\pi_\theta(y|x)}{\mu(y|x)} = \beta \sum_{t=1}^{T} \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})}\)

这样我们直接一步就得到了LLM。

二、 LLM ratio本质上是一个Q-function

那么问题来了，假设我们最终目的仅仅是为了得到一个奖励函数 \(r_\theta\) ， 而不是为了得到一个 \(\pi_\theta\) 。我们还有必要用DPO这套方法来建模 \(r_\theta\) 吗？

• $ r_^$ = 上面定义式。它由两个LLM来表征
• \(r_\theta^\text{raw}\) = 一个单独的神经网络。就像RLHF种的普通reward model 那样输入一整条句子，输出一个标量。

这两个参数化建模 \(r_\theta\) 的方式，不考虑计算速度，显存需求，网络架构这些empirical 区别，有理论上的本质差异吗？

----有！简单讲 \(r_\theta^\text{DPO}\) 有一个极其好的数学性质：那就是 \(E_{\mu(y_{>t}|y_{\leq t})}e^{r_\theta^\text{DPO}(y) / \beta}\) 这个期望会非常好计算，它不需要我们真的求数学期望，而是有严格解析解的。我们定义新符号 \(Q_\theta(y_t|y_{< t} ) := \beta \log E_{\mu(y_{>t}|y_{\leq t})}e^{r_\theta^\text{DPO}(y) / \beta}\) ,这个符号所代表的物理量满足下面的性质：

\(Q_\theta(y_t|y_{< t} ) = \beta \sum_{i=1}^{t} \log \frac{\pi_\theta(y_i|y_{<i})}{\mu(y_i|y_{<i})}\)

证明（这个证明无法省略，是算法叙述的核心）：

当t=T-1时候，我们有 \(Q_\theta(y_{T-1}|y_{< T-1} ) := \beta \log E_{\mu(y_T|y_{\leq T-1})}e^{r_\theta^\text{DPO}(y) / \beta} \\= \beta \log E_{\mu(y_T|y_{\leq T-1})}e^{\sum_{t=1}^{T} \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})}} \\ = \beta \log E_{\mu(y_T|y_{\leq T-1})} \prod_{t=1}^{T} \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})} \\ = \beta \log \prod_{t=1}^{T-1} \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})} E_{\mu(y_T|y_{\leq T-1})} \frac{\pi_\theta(y_T|y_{<T})}{\mu(y_T|y_{<T})}\\ = \beta\sum_{t=1}^{T-1} \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})} \\\)

当t<T-1的时候，可以类似用数学归纳法证明。

认真看完证明公式你会发现， \(Q(y_t|y_{< t} ) := \beta \log E_{\mu(y_{>t}|y_{\leq t})}e^{r_\theta^\text{DPO}(y) / \beta}\) 这个看似intractable的物理量可以解析表示的核心原因就是 \(r_\theta^\text{DPO}\) 本质上是由两个通过softmax自归一化的生成式模型表征的。把 \(r_\theta^\text{DPO}\) 替换为传统的 \(r_\theta^\text{raw}\) 你不可能得到类似的性质。（你想吧，如果你的打分函数 \(r_\theta^\text{raw}\) 只能对一整个句子打分，得到一个scalar rew，现在给你半个句子，为了计算上面那个期望，你是不是只能先用 \(\mu\) 采样无数句子，再对这无数个句子打分然后取“平均”得到 \(Q_\theta(y_{T-1}|y_{< T-1} ) ？）\)

三、上面Q-function的物理含义

总结上一节的内容：我们先定义了一个新的物理量

\(Q(y_t|y_{< t} ) := \beta \log E_{\mu(y_{>t}|y_{\leq t})}e^{r(y) / \beta}\)

我们发现，当且仅当 \(r(y):=r_\theta^\text{DPO}(y)\) 时， \(Q_\theta(y_t|y_{< t} ) = \beta \sum_{i=1}^{t} \log \frac{\pi_\theta(y_i|y_{<i})}{\mu(y_i|y_{<i})}\) 在解析意义上严格成立，可以轻易计算。

你可能会问： “ok，我们现在可以轻易算出来一个原本intractable的物理量。so what？ \(Q(y_t|y_{< t} )\) 有什么物理含义吗？”

我先给出答案：说白了 \(Q(y_t|y_{< t} )\) 这个函数输入LLM模型的前t个toekn的logp ratio之和，输出表示的是对前一半句子 \(y_{< t}\) 的打分，Q exactly就是强化学习(softRL)中的Q-function。而我们传统认为的reward model只是Q在t=T时候的特例。当t=T时，我们有 \(Q(y_T|y_{< T} ) = r_\theta^\text{DPO} (y)\) 。

这个牛逼的点就在于：如果你用DPO的方法来训练reward model，在训练的时候你输入给神经网络的全部都是一整条的句子，learning target是一个句子的reward。而evaluation的时候，你可以只输入给神经网络前一半句子，这个model自动就会变成半个句子的Q-function。而这一切都是有强理论保证且exactly精确的。回忆下PPO算法中，学一个类似的Q-function，为了算GAE你是不是得在训练中给Value model要喂半个句子（随机truncate得到）的数据？即使这样它学到的神经网络也只是“近似”的而已。

这个巨大的差别本质上就是因为我们在用两个generative model来表征一个函数，而生成式模型的“自归一化”（self-normalization）性质，带来了很多理论的好处。

四、Q-function用于credit assignment的empirical理解

\(Q(y_t|y_{< t} )\) 实际有什么用呢？我为什么非要把他记为 \(Q(y_t|y_{< t} )\) 而不把它记为 \(Q(y_{\leq t} )\) 呢？

想象一个场景，如果我们现在正在用LLM生成一个句子，并且一直用 \(Q_\theta^\text{DPO}\) 监测评估已经生成句子的分数，设句子在第100步出现了EOS token而终止。我们作图如下：

根据定义，Q的物理含义就是，“立足我已经生成的一半句子 \(y_{\leq t}\) ，我对于我未来完整句子能拿多少分数的一个预期”。随着t的增加，我们这个分数估计会越来越准确，在t=T时，我们的估计就是100%准确的。

那么如果我们生成了一个新的token，然后发现Q增加了，那这是不是就严格说明这个token是“好”的？ 反之，如果我们发现Q大幅度下降，我们是不是就知道这个token“非常有害”？

而一个token对于Q值造成的difference，其实在DPO setting下可以精确计算的：

\(Q_\theta(y_t|y_{< t} ) = \beta \sum_{i=1}^{t-1} \log \frac{\pi_\theta(y_i|y_{<i})}{\mu(y_i|y_{<i})} + \beta \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})} = Q_\theta(y_{t-1}|y_{< t-1} ) + \beta \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})}\)

\(\Delta Q(y_t| y_{<t}) = \beta \log \frac{\pi_\theta(y_t|y_{<t})}{\mu(y_t|y_{<t})}\)

这里的 \(\Delta Q\) 就是一个token 的credit。 \(\Delta Q\) 太低就意味着我们当下生成的token对系统影响是不利的。所有token的“credit”之和就等于我们这一条句子的真实reward。

DPO原文的第一个实验也正是在做这样credit的分解。

为了加强理解，我们再想象另外一个场景，如果我们还用LLM \(\mu\) 生成句子，且已经生成了一半 \(y_{<t}\) 。下一步我们要生成 \(y_t\) 这个token了。vocabulary只有两个单词， \(y_t^1\) 和 \(y_t^2\) 。我现在想知道，如果我希望尽可能提高最终句子得高分的概率，那我到底是应该选 \(y_t^1\) 还是 \(y_t^2\) 呢？答案是你应该选 \(Q(y_t^1|y_{< t} )\) 和 \(Q(y_t^2|y_{< t} )\) 值更大者。而在 \(r_\theta^\text{DPO}(y) = r(y)\) 场景下，这两个物理量的比较式很容易的，因为你可以忽略他们公共部分，只比较 \(y_t^1\) 和 \(y_t^2\) 的 credit。基于这个理解，我们可以用这个来进行句子采样中的“planning”搜索，这也正是原文第二个实验应用。

总结下这一小节，DPO在理论上基本严谨地完成了这么一个任务。就是给你一个sparse reward标注的数据集，在有足够多（指数级）的数据情况下，你可以训练得到一个模型，把稀疏的奖励合理分摊到每一个token上，从而把sparse rew问题转移为dense rew问题。（严谨理论后面再讨论）

四、上面Q-function的强化学习定义

（这是进阶内容，不太关心理论的同学可跳过，主要解释原文常提及的bellman consistency啥意思，需要简单RL基础）

首先我们把LLM建模成为一个MDP决策问题，每产生一个token是一步action，当下的state则是已经产生的所有token（前一半句子），产生T个token序列终止。这个episode中reward是稀疏的，只在最后一步得到:

\(r(y) = r(y_1) + r(y_2|y_1) + .... + r(y_{T-1}|y_{T-2}) + r(y_{T}|y_{T-1}) = 0 + 0 + ... 0+ r(y)\)

我们在这个MDP环境中用强行定义 \({V^\mu}\) 函数和 \(Q^\mu\) 函数。这组定义式我们称为叫做Bellman Equation：

\(Q^\mu(y_t|y_{<t}) := r(y_t|y_{<t} ) + \gamma V^\mu(y_t) = V^\mu(y_{\leq t}) \quad \text{if}\quad y_t \neq \text{EOS}.\)

\(Q^\mu(y_t|y_{<t}) := r(y_t|y_{<t} ) + \gamma V^\mu(y_t) = r(y)\quad \text{if}\quad y_t = \text{EOS}.\)

\(V^\mu(y_{<t}):=\beta ln E_{\mu(y_{t}|y_{<t})} e^{Q(y_{t}|y_{<t})/\beta}\)

上面的定义式中间部分都是在dense reward场景下严格定义的。右侧式子，则是MDP在稀疏奖励且 \(\gamma=1\) ，也就是LLM应用中的特殊情况下得到的。

你可以把上面的定义式从t=T到t=0一步步数学归纳展开，可以得到下面的结论

\(V^\mu(y_{<t}) =\beta ln E_{\mu(y_{\geq t}|y_{<t})} e^{[r(y_t|y_{<t}) + .... + r(y_{T-1}|y_{T-2}) + r(y_{T}|y_{T-1}) ]/\beta} =\beta ln E_{\mu(y_{\geq t}|y_{<t})} e^{r(y) /\beta}\)

\(Q^\mu(y_t|y_{<t})=\beta ln E_{\mu(y_{> t}|y_{\leq t})} e^{r(y) /\beta}\)

到此为止，你可以自行验证，只要我能学到一个精确的 \(r_\theta^\text{DPO}(y) = r(y)\) ,并且定义 \(Q_\theta(y_t|y_{< t} ) = \beta \sum_{i=1}^{t} \log \frac{\pi_\theta(y_i|y_{<i})}{\mu(y_i|y_{<i})} ， V_\theta(y_{\leq t} ) = \beta \sum_{i=1}^{t} \log \frac{\pi_\theta(y_i|y_{<i})}{\mu(y_i|y_{<i})}\) ,那么 \(Q_\theta=Q^\mu , V_\theta=V^\mu\) 就自动成立了。这一切只需要我用DPO的方法搭建神经网络。

这也是原文反复说什么有他们方法有bellman consistency的含义。

问：PPO RLHF中我们需要用到一个 \({V^\mu}\) 函数，它定义是 \(V^\mu(y_{<t}) := E_{\mu(y\geq t|y_{<t})} r(y)\) ，似乎和上面定义不一致啊？

这个新的bellman定义并非空穴来风，有较深层的RL理论保证（原文Eq 5），是经典理论。感兴趣可以参考到X-QL，softQL，SAC等论文。X-QL一作也和本文一作重合，我记得是去年ICLR的oral。

\(V^\mu(y_{<t})|_{\beta} =\beta ln E_{\mu(y_{\geq t}|y_{<t})} e^{r(y)/\beta}\) 也可以称为一个value function, 只不过它不再是简单平均期望，而是指数意义下期望（softmax而非mean）:

\(E_{\mu(y\geq t|y_{<t})} r(y) =V^\mu(y_{<t})|_{\beta \to \infty}<\beta ln E_{\mu(y_{\geq t}|y_{<t})} e^{r(y)/\beta} < V^\mu(y_{<t})|_{\beta \to 0} = r^\text{max}_\theta(y)|_{\mu(y_{\geq t}|y_{<t})}\)

问：这种训练方法对RL领域有何启示？

我个人认为，off-policy算法的核心痛点在于Q函数很难学。它往往需要用bellman公式来进行bootstrapping训练，这导致了训练的极其不稳定，才有了16-18年各种各样的优化trick（如target network和twin delayed update）。DPO给出了一种generative model for discriminative task的Q-learning范式，可能有其意义。

五、DPO训练中chosen response的logp ratio在训练中下降问题。

我相信绝大多数实操过DPO训练的同学都会发现一个反直觉的现象。就是看logp的评估曲线，你会发现无论数据还是测试集中被preferred的数据，经过DPO finetune后被sample到的概率反而下降，而不是上升了。只不过那个rejected response的logp下降的更快，才让loss function持续下降（因为reward margin上升了）。

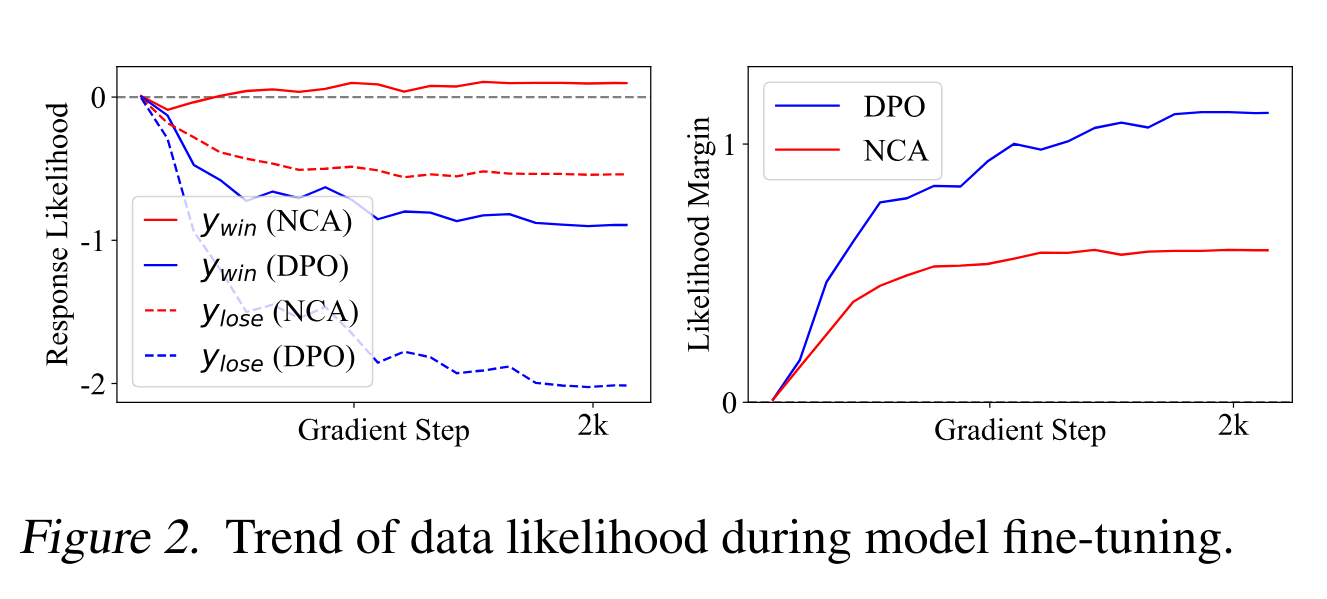
这篇文章第三个实验，给这个现象进行了一些合理性分析，但并没有给出理论上的解决方案，因此希望在这里给我们的工作打个广告（图穷匕见）。

1
2

Noise Contrastive Alignment of Language Models with Explicit Rewards
https://arxiv.org/abs/2402.05369

这篇工作里，我们从contrastive learning的视角，基于NCE算法严格推导得到了一个更加general的LLM alignment方法。它不仅可以处理preference二元数据（y_w>y_l)，还可以处理任意多个的由explicit scalar reward标注的reponse数据，可以充分利用分差信息。这篇文章中提出的NCA算法，应该是首次提出并从理论和实践两个层面都解释并解决了DPO算法chosen response 的logp下降的问题。（虽然并没被引用）

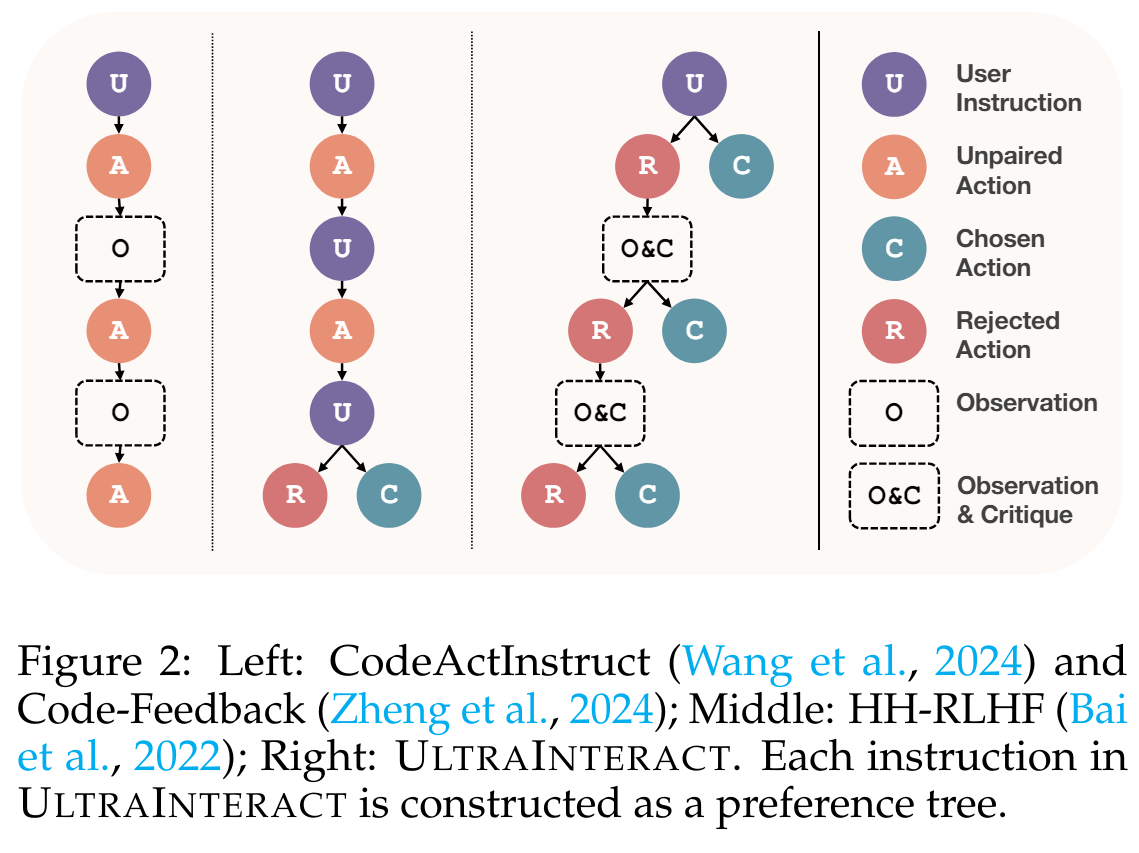
在工程实践中，THUNLP实验室的一篇工作在他们提出的tree-structure reasoning数据集UltraInteract上对我们的方法进行了独立的第三方评测，并于KTO和DPO算法进行了对比。发现NCA在70B模型上表现最优，在数理代码等指标上接近或超过了GPT3.5的水平。

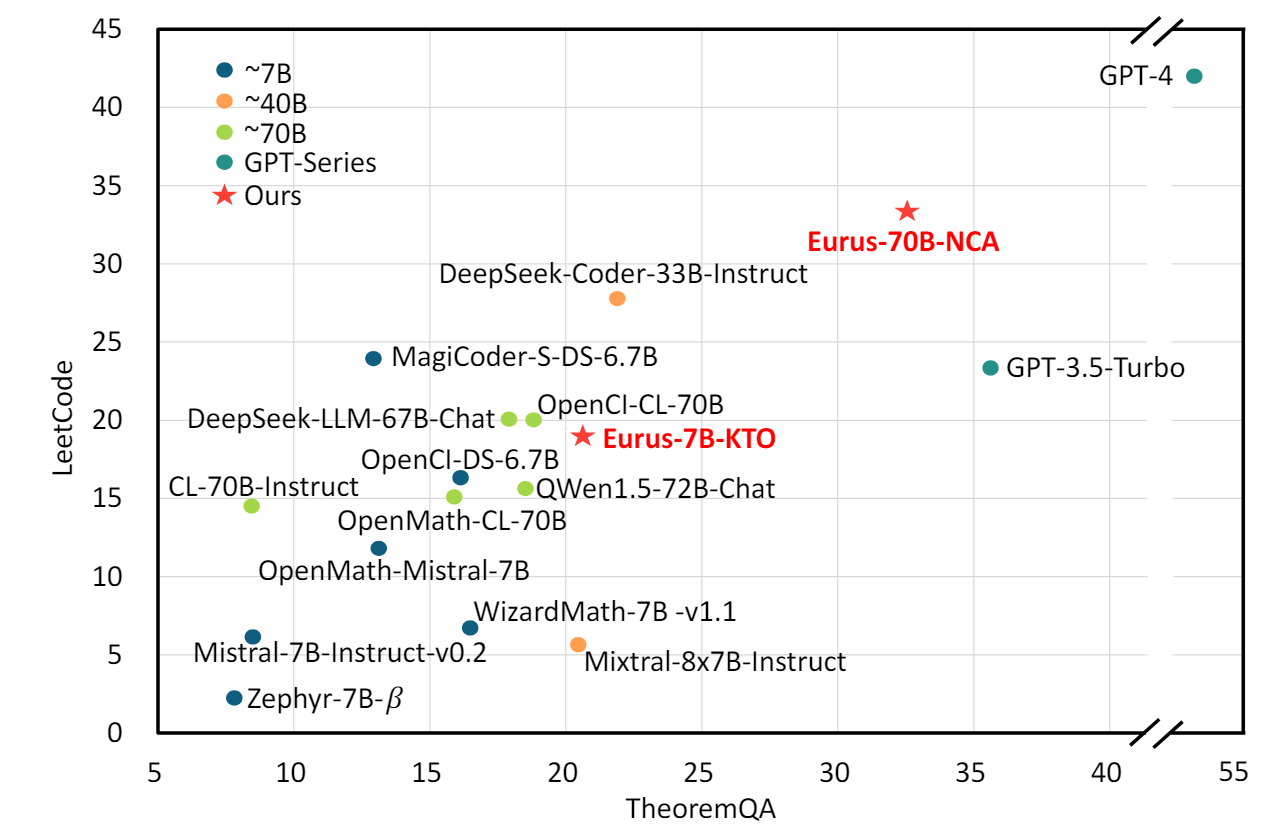
此外，UltraInteract这个数据集在我看来部分解决了from r to Q*这篇文章走向应用的一个痛点：目前没有dense-reward标注的response数据集。虽然UltraInteract也无法对句子进行per-token level的质量标注，但是他们采用逐阶段标注打分标注的方法也依然可以视为某种trade-off。这应当是符合LLM 从sparse reward setting走向dense reward的趋势的。