大家好，这里是减论系列专栏，《从分布到生成》专题第二集。

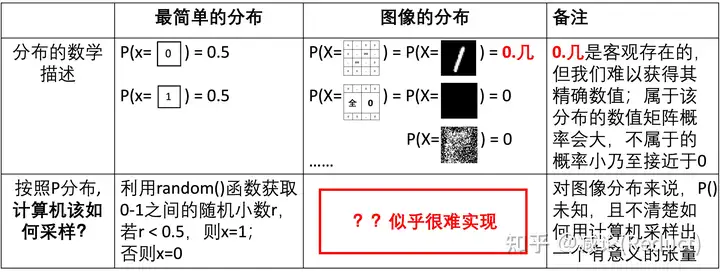
上回说到，如图一所示，简单的分布例如伯努利分布、均匀分布、高斯分布都可以借助程序语言中的random(), normal()等基础的伪随机函数进行计算机采样模拟。然而，服从特定的分布P(X)的图像（例如0-9黑白数字图像）却似乎很难借助计算机的某个函数采样实现，这个难点体现在2个方面：

• 我们很难知道具体的图像分布P(X)；
• 即使我们知道了图像分布P(X)精确值，如何通过程序进行一次性采样并能服从P(X)也不清楚。

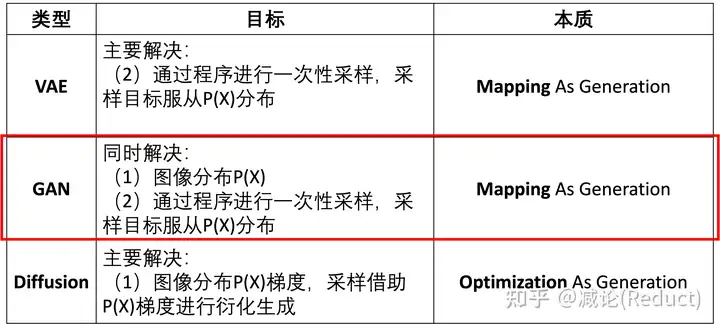
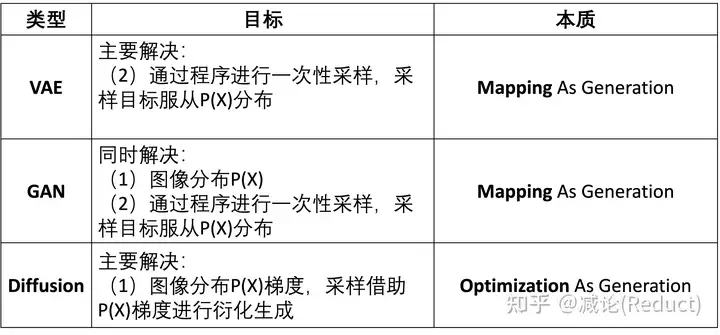
为了解决从某个特定分布P(X)进行图像采样的任务（即图像生成任务），业界进行了长期的努力并衍生出3大主要流派：VAE（变分自编码器）、GAN（对抗生成网络）和Diffusion（扩散模型）。在图二中，我们将这三个流派与上述两个难点进行关联，看看各自都是从哪个难点入手进行解决的。

接下来的事情就比较有趣了。

从本质上来看：

• VAE尝试重点解决第二个难点（2），通过程序进行一次性采样，采样目标服从P(X)分布，具体是通过映射来一步采样生成（Mapping As Generation）；
• GAN尝试同时解决上述2个难点（1）（2），其同时建模了图像分布P(X)，并也是通过映射来一步采样生成（Mapping As Generation）；
• Diffusion则重点解决第1个难点（1），并尝试从（1）的结果中迭代出图像，通过优化来逐步生成（Optimization As Generation）。

这里提到的“映射”“优化”如何理解，下文及后续的专集会给出具体的阐述。本集我们先从VAE说起。VAE试图重点解决：“通过程序进行一次性采样，采样目标服从P(X)分布”。

计算机程序能够很容易地采样简单分布中的样本；但很难采样复杂图像，那么一个最为朴素的做法就是：

我让简单分布中的所有样本x，都与复杂图像中的所有样本X，形成一个映射x -> X: X = F(x)，这样计算机不就可以仅仅通过采样简单分布中的样本x，利用该映射F(x)直接获取图像样本X了嘛！

我们先从一个最简单的情况来理解这个映射过程，其中x服从均匀分布，X服从正态高斯分布，如图三所示：

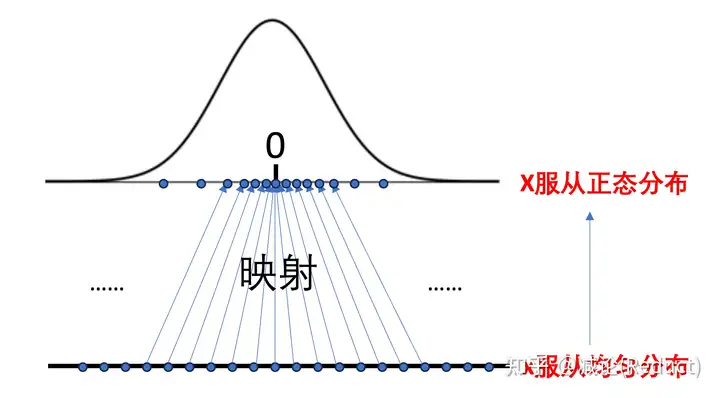
在图三中，所有均匀采样出来的x，通过映射函数，得到的X的样本即符合正态分布。这意味着，有很多均匀采样出来的x被映射之后的数值X都会往中间那个数值0靠拢，因为对于正态分布而言P(X = 0)以及X=0附近的数值概率是偏大的，在0值附近采样出来样本的概率自然也是更大的。

下面，我们进一步把X复杂化为高维度的图像样本，如图四左侧展示了一种可能的映射方式，将[0,1]均匀分布采样的一个数字样本映射到1,3,5,7,9的所有奇数数字图像样本上：

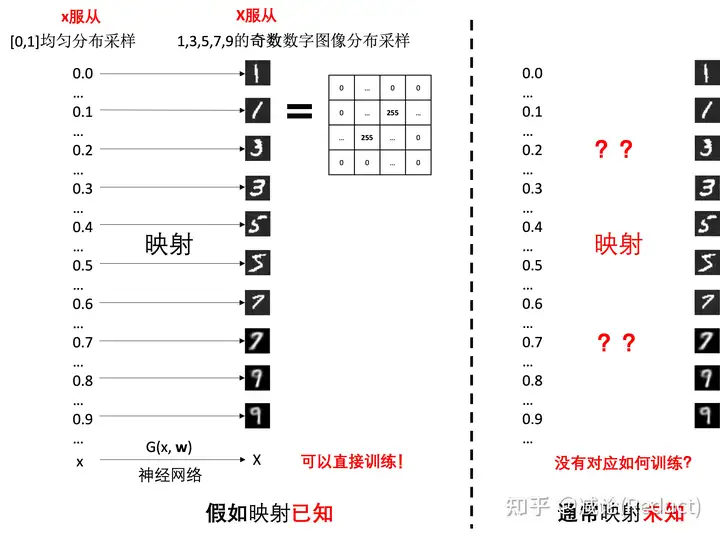
假设当我们明确知道了这个映射，也就是如图四左侧所示，所有观测到的奇数数字图像都能找到一个明确的[0,1]均匀分布中采样的数值对应，那么我们就拥有充足的样本对，即可以直接借助神经网络G(x, w)来学习这个映射X = G(x, w)，其中w是可学习参数。

当然，作为解决生成任务的方案，我们通常希望这个神经网络G能够具有的一些比较理想的性质是：

• 我们采样输入训练中未曾见过的[0,1]均匀分布中的数值，假如是0.85，网络也能输出接近某个特定数字但是又有些区别的图像（产生生成新图像效果）：

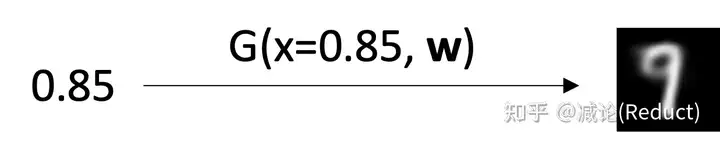
• 输入数值之间的微小变化能够对应到图像语义上的相对平滑的过渡；即输入相近，输出的图像相似（具有一定的输入可控性以及语义一致性）：

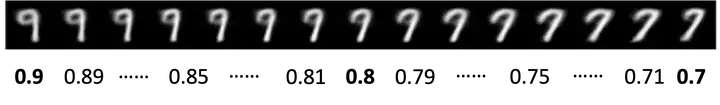
我们再来理解一下这个神经网络G。严格意义上来讲，这里的G并不直接建模数据的分布；它只负责样本x与样本X间的映射，而且通常是易采样的样本x到复杂高维的不易采样的样本X。我们通过从x的分布P(x)大量采样x，通过X=G(x,w)能够生成大量的X，然后这些X恰好能够符合我们专栏第一章提到的图像的分布P(X)。

再联系到现有技术本身，这个神经网络G其实就是VAE中的解码器Decoder（也是GAN中的生成器Generator，在专题下一集中详述）的角色，其负责将易采样的样本x映射到复杂高维的样本X，且我们期望通过大量采样并映射后，样本X的确是服从某个特定图像分布的。

但是！！！！！！如图四右侧所示，在绝大部分情况下，我们是无法提前安排好或者知道这个映射的，也就是说，我们并不知道哪些均匀分布的数值x样本对应哪些图片X样本。

有人可能会问：我们随机分配一下这个映射行不行？答案大概率是不行的，主要有2点原因：

• 完全随机分配不一定能保证采样的图像满足其分布P(X)；
• 随机分配不一定保有上述提到的神经网络G采样的理想性质（a）和（b）。

那随机分配也不行的，我们怎么训练呢？很简单的，我们有一个非常直接的想法，如图五所示分三步走：

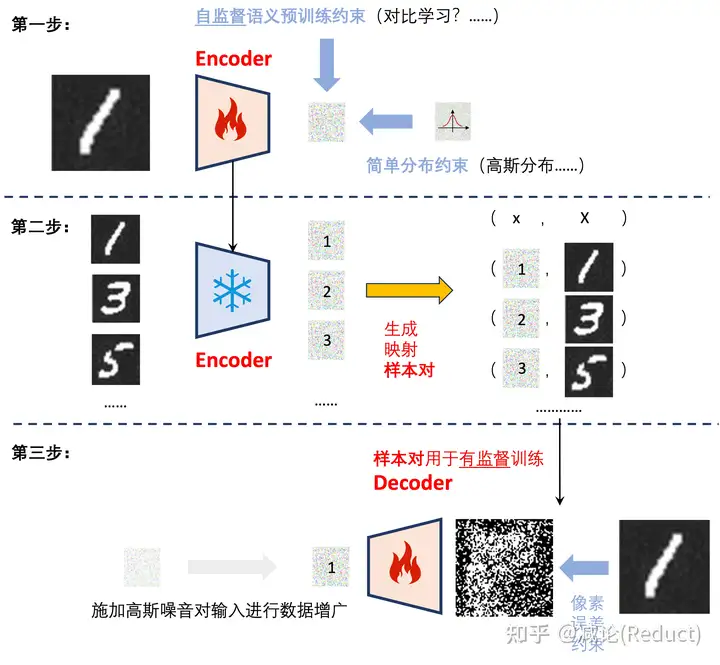
第一步： 可以借助预训练手段训练Encoder，对已观测的图片进行编码，并额外施加一个约束使得该编码服从一个特定的简单分布约束（这里我们以高斯分布为例），以便于后续采样使用；

第二步： 冻结Encoder，获得所有观测图片的编码，并将其组织成样本对（编码，数字图像）；

第三步： 利用这些样本对有监督训练Decoder。当然，我们在训练Decoder的实践过程中，为了让Decoder更加鲁棒，通常会对输入的编码施加一个高斯噪音进行数据增广以扩充训练空间。

三步进行完毕，最终我们可以利用Decoder，采样一个高斯分布作为输入，从而生成（采样）出预期的奇数数字的图像。

当然，如果我们更大胆一些，还可以一步到位，把三步融为一步，将Encoder和Decoder端到端地串起来，即把生成映射样本对的过程端到端地嵌入整个Encoder-Decoder网络训练过程中，如图六所示：

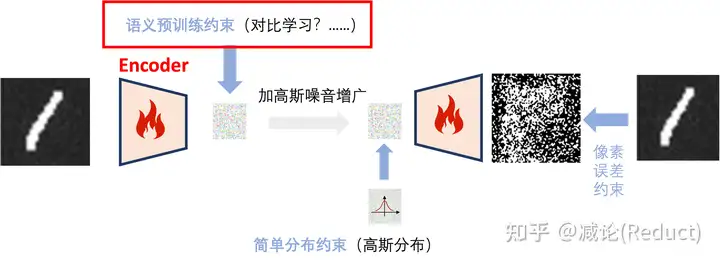
惊人的事情发生了！我们发现，如果我们将三步合为一步，那么整个模型几乎就完全变成了VAE的结构，唯一多出来的一项则是红框中一种约束语义的损失，即相似的图像其编码也要相近。

总结一下，本集从最为基础的“样本映射”视角，无任何概率理论地导出了VAE的架构，并给出了一种基础的扩展形式（即增加语义一致性损失进行约束），希望能给大家带来一定的启发。一家之言，恐有纰漏，还望多多建议与探讨。