大家好，这里是减论8分钟极减专栏系列，《从分布到生成》专题第三集。本集信息量极大，观点视角极度新颖炸裂，请大家屏住呼吸，别眨眼，且听我慢慢道来。

在“从分布到生成（一、二）”中，我们已经带领大家极减地理解了什么是图像的分布P(X)，以及如何使用映射来采样生成复杂分布的样本。还不清楚的小伙伴可以移步一、二系列内容进行学习。

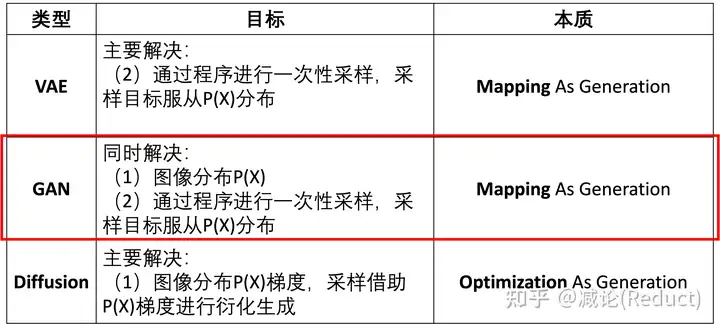
本次专题第三集，我们来尝试回答GAN是如何同时解决那两个采样难题的（图一红框所示），即：

• • 如何找到图像分布P(X)？
• • 如何通过程序进行一次性采样，采样目标服从P(X)分布？

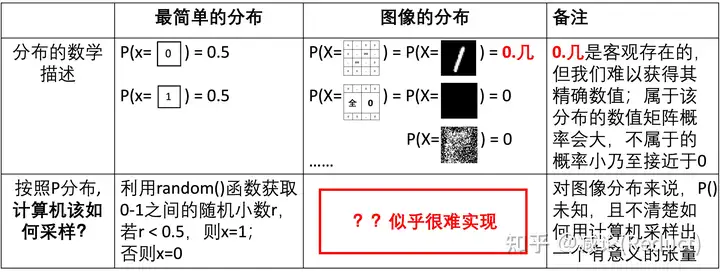
此前我们提到过，图像分布P(X)非常复杂，精确地求出每个P(X=…) = …的概率数值通常是不现实的，另外很精确其实也没有太大的必要。那么我们把思路做一下简化：

假设我们已经知道了P(X)，并且是用神经网络D(X,w’)来逼近表示的，其中w’是该神经网络固定的参数。我们每输入一个张量实例X，都能通过D(X,w’)得到其准确的概率数值：P(X) = D(X,w’)，如图二所示：

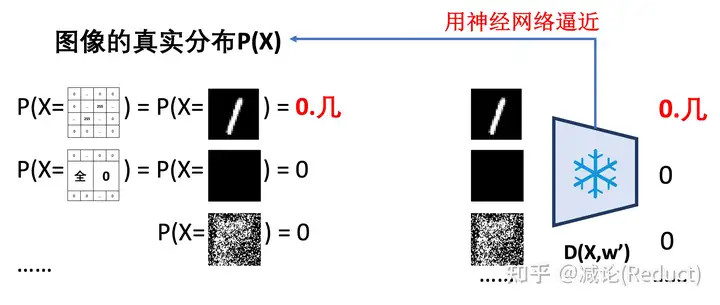
那么，当我们知道了用神经网络D(X,w’)来逼近表示的图像分布P(X)有什么用处呢？哦，这可太有用了。如果P(X)已知且用神经网络D(X,w’)表示了，我们就又可以规避掉“从分布到生成（二）”中提到的无法安排两个分布采样的样本之间的分配映射问题。实际上，我们利用D(X,w’)网络产生监督信号，从而可以自动地为每一个从简单分布中采样的样本x寻找其合适的映射图像X！

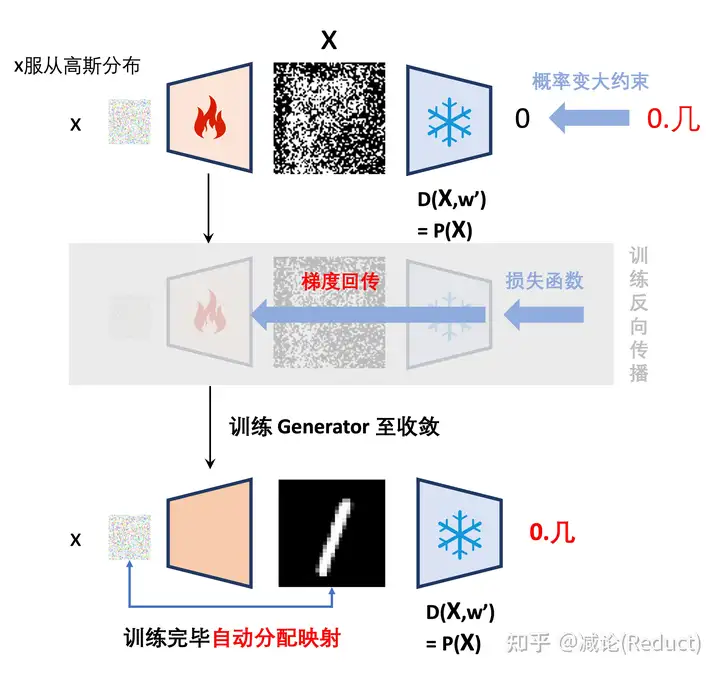
具体操作如图三所示。我们从高斯分布中采样x，经过可训练的Generator（即G(x,w)）生成张量X=G(x,w)，而张量X如果要服从图像分布P(X)，那么其输入D(X,w’)中得到的输出数值则要偏大，这样我们就形成了损失约束，通过整个梯度回传来优化更新Generator。当所有的x都能通过Generator生成符合图像分布P(X)的X样本，最终的输出将不再有误差，末端的损失函数即为0，此时网络不再产生梯度，从而收敛，并且自动化地构建了输入样本x与输出图像X的映射。

这里有个小细节说明一下。此前我们一直用“0.几”来代表一个分布内图像的概率数值，是因为考虑到了离散概率求和为1的约束。但实际上，这个约束在这个场合中没有那么重要，因为我们主要用于采样，概率分布通常只要满足相对性关系即可：P(X=分布内图像) > P(X=分布外图像) 。所以在实操中，我们通常也可以将“0.几”简单地替换为1来理解或实践。方便起见，后文我们用“1”来代替“0.几”的表述。

非常有趣的是，图三所述的过程，几乎就是GAN中Generator所扮演的全部角色，我们也回答了GAN解决的第2个难点“（2）如何通过程序进行一次性采样，采样目标服从P(X)分布？”。

接下来，我们再看第1个难点，即回到之前推理过程中唯一难满足的那个条件假设：“假设我们已经知道用神经网络D(X,w’)来逼近表示的P(X)”。是的，我们怎么能得到已知的逼近于真实图像分布P(X)的D(X,w’)呢？

其实仔细思考一下，虽然作为图像分布P(X)的确很难精确表示，但要知道，根据万能逼近定理，这个世界上还没有啥神经网络拟合不了的函数，而图像分布P(X)也仅仅是大千世界中的一个小小的复杂函数而已。另外，根据上文所述，在我们采样生成的任务背景下，P(X)函数通常不需要很精确的建模，仅需要满足相对性关系就足够我们采样了（我们也称其为广义的图像分布函数）：

1 = P(X=分布内图像) > P(X=分布外图像) = 0

方便起见，我们就让分布内的概率数值趋近1，分布外的趋近0即可。趋近1的我们也简称为正样本，趋近0的我们简称为负样本。要训练一个神经网络来逼近P(X)函数，基本操作就是收集足够多、足够丰富多样的正负样本进行训练即可：

正样本：正样本很容易获取，就用我们实际采集到的观测图像，例如奇数灰度数字图像即可；

负样本：最关键的问题来了，负样本从何而来？

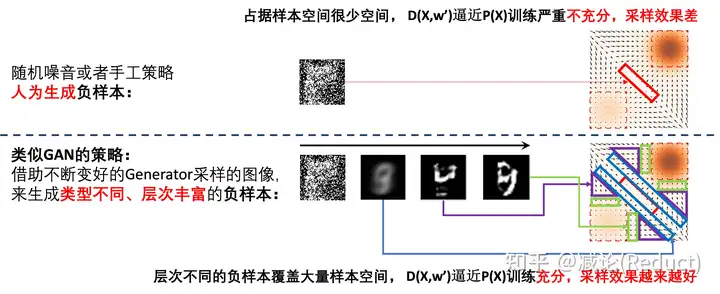
关于负样本，有小伙伴可能会说，我们通过随机噪音采样人为生成一些负样本可以不？这当然是可以的，不过有一些问题，这些样本在整个P(X)的X取值空间中仅仅占据很小的一个空间部分（如图四上方所示），而且通常距离正样本很远（很不相似），会导致D(X,w’)逼近P(X)的训练严重不充分，采样效果也会很差。

此时，类似GAN策略的精髓就体现出来（如图四下方所示）：我们借助不断变好的Generator采样的图像，来生成类型不同、层次丰富的负样本。

我们先看最开始，Generator网络随机初始化后，通过Generator采样只能采样出类似于随机噪音的图像，与之前说的人为生成负样本并无区别；我们用这些图像先作为负样本，虽然此时D(X,w’)逼近P(X) 训练极不充分，但是也能训练出一个非常粗糙的D(X,w’)分布，它的采样效果，也就是其对应Generator的能力很差，但大概率已经能比噪音图像好一些，例如它能够生成一个很模糊的9。这些类似于很模糊的9的图像就充当了新一层次的负样本，扩充了D(X,w’) 的整个训练空间，从而让D(X,w’)逼近P(X) 的训练变得更充分了一些，也更精准了一些，从而反过来来提升Generator的采样能力。如此迭代往复，最终D(X,w’) 训练的很充分，非常逼近于真实图像分布P(X)，那么参考图三，其对应的Generator自然也能采样出很好的服从P(X)分布图像。

用更精炼的语言来组织这个算法过程：

• • Generator为D(X,w’)的训练提供尽可能多且丰富的负样本，使D(X,w’)能够越来越充分地训练并不断逼近最终的真实图像分布P(X)。
• • D(X,w’)在不同的训练阶段以不同的程度接近于真实图像分布P(X)，其不同的阶段我们都会训练出服从D(X,w’)分布的采样器Generator。

如此迭代往复即可。

我们可以看到，这个过程与GAN的算法流程在代码实现上是一致的，但是理解的视角却是完全不同：这个过程看上去不是一个对抗过程，而是一个相辅相成、互相促进的过程：Generator为Discriminator提供更丰富的负样本，使得Discriminator越来越逼近真实的图像分布P(X)；同时，Discriminator也会得到其当前分布状态下对应的采样器Generator，如此循环。

有了这些理解，我们惊人地发现我们能够非常直观地解释很多GAN本身的问题（例如GAN不收敛、模式崩溃、生成器和判别器之间的不平衡导致过拟合等等），并且能够提出很多此前的理解无法想象到的改进。因为这块内容非常多，可以独立成一章，在本集中我们暂不展开，各位小伙伴可以先提前自己思考，并欢迎打在评论区探讨。

Take Home Notes

1. GAN中的Discriminator可以理解为广义的图像分布函数；

2. GAN可以理解为一个非对抗的相辅相成过程：Generator为Discriminator提供更丰富的负样本，使得Discriminator越来越逼近真实的图像分布P(X)；同时，Discriminator也会得到其当前分布状态下对应的采样器Generator，如此循环。

3. GAN最终目标可以是让Discriminator完美逼近于真实的(广义)图像分布P(X)。